La interferencia electromagnética o EMI es uno de los principales enemigos de los equipos electrónicos y se puede presentar en cualquier lugar y momento causando problemas, daños y perdidas imprevisibles. La EMI se puede manifestar de muchas maneras; por ejemplo cuando cae un rayo y este genera transientes o picos de voltaje muy elevados que dañan los equipos electrónicos, también aparece cuando los equipos se encuentran cerca de una fuente emisora electromagnética potente como puede ser una radio emisora o una estación de TV.A las causas de la Interferencia Electromagnética las podemos clasificar en dos categorías: los transientes (transitorios) y las señales constantes.Transientes.- Son fenómenos puntuales y únicos, pueden presentarse uno detrás de otro o juntos, que se caracterizan por ser pulsos de gran cantidad de energía y de muy corta duración con muy cortos tiempos de subida y bajada de la señal. |
Electromagnetic Compatibility. EMC Requirements for Electronic Systems. Signal Spectra—the Relationship between the Time Domain and the Frequency Domain. Representation of Nonperiodic Waveforms. Transmission Lines and Signal Integrity. Nonideal Behavior of Components. Conducted Emissions and Susceptibility. Measurement of Conducted Emissions. Antennas. Elemental Dipole Antennas. Radiated Emissions and Susceptibility. Simple Emission Models for Wires and PCB Lands. Crosstalk.
lunes, 15 de febrero de 2010
EMI
Etiquetas:
Vanessa Gaviria
Ruido Eléctrico
El ruido eléctrico, también llamado interferencia electromagnética, o EMI, es una señal eléctrica despreciable que produce efectos indeseables y por otro lado trastornos en los circuitos de un sistema de control. La interferencia electromagnética o EMI puede ser radiada o conducida. Cuando el ruido que se origina en una fuente y viaja a través del aire se le llama radiación de EMI. Las señales de radio y TV pueden ser fuentes de radiación de EMI. El ruido conducido viaja a través de un conductor, como una línea de energía. El ruido original puede haber sido radiado, depositado en las líneas y entonces conducido.La interferencia es una característica típicamente ondulatoria, que es el origen de fenómenos inexplicables desde perspectivas corpusculares. Aparentemente, la superposición de luz conduce a su aniquilación en algunos casos o a la multiplicación energética, por encima de la contribución de cada fuente, en otros. Estas aparentes paradojas se explican mediante la interferencia.Los fenómenos de interferencia, junto a los de difracción, son los más característicos de las ondas y no están presentes en la dinámica de partículas. Por esta razón desempeñaron un papel central en las discusiones sobre la naturaleza de la luz.Dada la linealidad de la ecuación de ondas, su solución, cuando existen varias fuentes, puede obtenerse sumando las soluciones para cada una de las fuentes. Dado que la solución de la ecuación de ondas es la amplitud de onda, y que ésta es una función del espacio y del tiempo, la superposición siempre conduce a campos espaciales variables en el tiempo. Esta combinación de soluciones se denomina interferencia. En algunas ocasiones las amplitudes resultantes pueden resultar permanentemente nulas en algunas superficies, sin serlo ninguno de los sumandos, dando lugar a las franjas de interferencia.FUENTES DE INTERFERENCIA ELECTROMAGNÈTICAEl ruido en las líneas eléctricas es el problema más común y las fuentes que la causan son múltiples. Entre las fuentes a considerar están:• Interrupción de cargas |
Etiquetas:
Vanessa Gaviria
Antenas
La definición formal de una antena es un dispositivo que sirve para transmitir y recibir ondas de radio. Convierte la onda guiada por la línea de transmisión (el cable o guía de onda) en ondas electromagnéticas que se pueden transmitir por el espacio libre. En realidad una antena es un trozo de material conductor al cual se le aplica una señal y esta es radiada por el espacio libre. Las antenas deben de dotar a la onda radiada con un aspecto de dirección. Es decir, deben acentuar un solo aspecto de dirección y anular o mermar los demás. Esto es necesario ya que solo nos interesa radiar hacia una dirección determinada. Esto se puede explicar con un ejemplo, hablando de las antenas que llevan los satélites. Estas acentúan mucho la dirección hacia la tierra y anulan la de sentido contrario, puesto que lo que se quiere es comunicarse con la tierra y no mandar señales hacia el espacio. Las antenas también deben dotar a la onda radiada de una polarización. La polarización de una onda es la figura geométrica descrita, al transcurrir el tiempo, por el extremo del vector del campo eléctrico en un punto fijo del espacio en el plano perpendicular a la dirección de propagación. Para todas las ondas, esa figura es normalmente una elipse, pero hay dos casos particulares de interés y son cuando la figura trazada es un segmento, denominándose linealmente polarizada, y cuando la figura trazada es un círculo, denominándose circularmente polarizada. Una onda está polarizada circularmente o elípticamente a derechas si un observador viese a esa onda alejarse, y además viese girar al campo en el sentido de las agujas de un reloj. Lógicamente, si lo viese girar en sentido contrario, sería una onda polarizada circularmente o elípticamente a izquierdas. Distribución De Corriente En Una Antena Una antena, al ser un elemento de un circuito, tendrá una distribución de corrientes sobre ella misma. Esta distribución dependerá de la longitud que tenga la antena y del punto de alimentación de la misma. Una onda estacionaria es una onda que se crea cuando una señal se está propagando por un medio de transmisión y es reflejada por culpa de una mala adaptación o por culpa de un final de línea. Supongamos primero que tenemos una línea acabada en circuito abierto y alimentada en uno de sus extremos. En el momento de alimentar a esta línea de transmisión con una señal senoidal, se crea una onda que se propaga por la línea. Esta señal se irá repitiendo cada longitud de onda landa (una longitud de onda y no media longitud de onda) ya que es una señal senoidal y es periódica. Esto provoca que ahora tengamos una distribución de corrientes que no es constante y que varía en función de la longitud de onda landa. En la siguiente figura podemos ver una representación gráfica de como quedaría una distribución de corrientes en la línea que estamos tratando. Una vez que la onda llega al final de la línea, esta es reflejada al no poder continuar su camino, volviendo hacia el generador. Esta onda reflejada tiene un desfase de 90º respecto de la onda incidente, por lo que al sumarse con la onda incidente, tendremos puntos en donde la suma de un máximo y en donde de un mínimo. Esta suma de las dos ondas es la onda estacionaria que estamos buscando. Si en vez de estar acabada la línea en circuito abierto, estuviera acabada en corto circuito, también se reflejaría la onda, pero en vez de estar desfasada 90º, estaría desfasada 180º. También se sumaría a la onda incidente y lógicamente también creará la onda estacionaria. En la figura anterior observamos como quedan la onda incidente, la reflejada y la estacionaria en la línea de transmisión que estamos tratando. Esta es la onda estacionaria que se crea en la línea. Para entenderlo mejor se suele representar el módulo de la intensidad, que sería lo que mediría un medidor de corriente de RF, y la tensión en la misma línea. Una cosa que no se ha comentado, pero que es muy importante, es la posición de los máximos y de los mínimos de una onda estacionaria. Al estar acabada la línea en un circuito abierto, en ese punto no podrá desplazarse la corriente, luego el módulo de la corriente en el extremo de la línea tendrá un mínimo. Por la misma razón, la tensión en ese punto tendrá un máximo, ya que hay máxima concentración de energía. Al ir variando la tensión y la intensidad en la línea, la impedancia también irá variando. Este detalle es importante puesto que una vez que tengamos diseñada nuestra antena, dependiendo del punto en el que la alimentemos, tendremos distinta impedancia. Así por ejemplo, si tenemos un cable de 50 ohmios para alimentar una antena, nos interesará alimentarla por un punto que presente impedancia cercana a 50 ohmios para tener las mínimas perdidas por desacoplo de impedancias. Como podemos ver en la imagen anterior, el módulo de la corriente en la línea se repite cada media longitud de onda, que es la distancia que se utiliza para diseñar antenas. Pero, ¿por qué se utiliza esa longitud y no otra?. En realidad hay muchos tipos de antenas y cada una utiliza una parte distinta de la longitud de onda, así que dependiendo de la aplicación que queramos, del tipo de antena que queramos utilizar y de más factores (espacio, ... ) utilizaremos una medida u otra. Vamos a ver que ocurre cuando modificamos un poco nuestra línea de transmisión que estamos tratando. Vamos a suponer que alimentamos en un punto cualquiera y que tenemos creada una onda estacionaria en ella. En la siguiente figura tenemos representado de forma esquemática como quedará esa onda en nuestra línea, en donde se indica con flechas el sentido de las corrientes. Sin meterse en cuestiones físicas, si una corriente circula por un conductor, creará un campo eléctrico y magnético en sus alrededores. Luego nuestra corriente creará un campo eléctrico y magnético, pero como supondremos que la distancia entre los dos conductores que forman nuestra línea (S) es pequeña, no se creará una onda que se propaga, puesto que la contribución que presenta el conductor superior se anulará con la que presenta el conductor inferior. Pero si separamos en un punto los dos conductores, los campos que crean las corrientes ya no se anularán entre si, si no que se creará un campo eléctrico y magnético que formará una onda que se podrá propagar por el espacio. Según esto, dependiendo del punto desde el que separemos el conductor, tendremos una longitud en los elementos radiantes (H) variable. Al variar esta longitud, la distribución de corriente variará, y lógicamente la onda que se creará y se propagará. Hay que seguir observando que en los extremos seguimos teniendo un mínimo de corriente y que continúa repitiéndose cada media longitud de onda. Luego ahora podemos ver de forma gráfica, que si suponemos que nuestra antena son solo los elementos radiantes y que el punto en el que los hemos separado es el punto de alimentación de la antena, el módulo de la intensidad en el punto de alimentación varía y lógicamente, también varía la impedancia que presenta la antena. Veamos como se distribuye la corriente en función de la longitud de la antena (H) y su diagrama de radiación en la siguiente tabla. En ella se indica el ancho de haz a -3 dB, la directividad (D), la resistencia de radiación en el punto de máxima corriente (Rrm) y la resistencia en el punto de alimentación de la antena (Rre). Como podemos ver, no por tener una antena más larga logramos radiar mejor, lo único que conseguimos es variar el diagrama de radiación y la impedancia que presenta. En esta tabla vemos que una antena vertical de 5/8 longitudes de onda es una de las mejores, de las representadas, para hacer contactos a larga distancia (DX) puesto que es la que tiene el lóbulo de radiación más bajo y es la que presenta la directividad más pronunciada. Esta directividad nos indica que presenta una mayor ganancia en la dirección de propagación que se observa en el diagrama de radiación. 2. Parámetros generales de una antena Una antena va a formar parte de un sistema, por lo que tenemos que definir parámetros que la describan y nos permita evaluar el efecto que va a producir sobre nuestro sistema. Impedancia Una antena se tendrá que conectar a un transmisor y deberá radiar el máximo de potencia posible con un mínimo de perdidas. Se deberá adaptar la antena al transmisor para una máxima transferencia de potencia, que se suele hacer a través de una línea de transmisión. Esta línea también influirá en la adaptación, debiéndose considerar su impedancia característica, atenuación y longitud. Como el transmisor producirá corrientes y campos, a la entrada de la antena se puede definir la impedancia de entrada mediante la relación tensión-corriente en ese punto. Esta impedancia poseerá una parte real Re(w) y una parte imaginaria Ri(w), dependientes de la frecuencia. Si a una frecuencia una antena no presenta parte imaginaria en su impedancia Ri(w)=0, entonces diremos que esa antena está resonando a esa frecuencia. Normalmente usaremos una antena a su frecuencia de resonancia, que es cuando mejor se comporta, luego a partir de ahora no hablaremos de la parte imaginaria de la impedancia de la antena, si no que hablaremos de la resistencia de entrada a la antena Re. Lógicamente esta resistencia también dependerá de la frecuencia. Esta resistencia de entrada se puede descomponer en dos resistencias, la resistencia de radiación (Rr) y la resistencia de pérdidas (RL). Se define la resistencia de radiación como una resistencia que disiparía en forma de calor la misma potencia que radiaría la antena. La antena por estar compuesta por conductores tendrá unas pérdidas en ellos. Estar pérdidas son las que definen la resistencia de pérdidas en la antena. Como nos interesa que una antena esté resonando para que la parte imaginaria de la antena sea cero. Esto es necesario para evitar tener que aplicar corrientes excesivas, que lo único que hacen es producir grandes pérdidas. Veamos este ejemplo: Queremos hacer una transmisión en onda media radiando 10 KW con una antena que presenta una impedancia de entrada Ze = 50 - j100 ohmios. Si aplicamos las fórmulas P = |I|2 x Real[Ze] = |I|2 = P / Real[Ze] Obtenemos que |I| = 14.14 A. |V| = |I| x |Ze| = 14.14 x (50 - j100) = 14.14 x 111.8 = 1580.9 V. Si ahora logramos hacer que resuene la antena, tendremos que la impedancia de entrada no tendrá parte imaginaria, luego Ze = 50 ohmios. Aplicando las mismas fórmulas de antes obtenemos que la intensidad que necesitamos es la misma |I| = 14.14 A, pero vemos que ahora la tensión necesaria es |V| = 707 V. Con este pequeño ejemplo vemos que hemos ahorrado más de la mitad de tensión teniendo la antena resonando que si no la tenemos. No se ha dicho, pero se ha supuesto que la parte real de la impedancia de entrada de la antena no varía en función de la frecuencia. Eficiencia Relacionado con la impedancia de la antena tenemos la eficiencia de radiación y la eficiencia de reflexión. Estas dos eficiencias nos indicarán una, cuanto de buena es una antena emitiendo señal, y otra, cuanto de bien está adaptada una antena a una línea de transmisión. La Eficiencia de Radiación se define como la relación entre la potencia radiada por la antena y la potencia que se entrega a la misma antena. Como la potencia está relacionada con la resistencia de la antena, podemos volver a definir la Eficiencia de Radiación como la relación entre la Resistencia de radiación y la Resistencia de la antena: La Eficiencia de Adaptación o Eficiencia de Reflexión es la relación entre la potencia que le llega a la antena y la potencia que se le aplica a ella. Esta eficiencia dependerá mucho de la impedancia que presente la línea de transmisión y de la impedancia de entrada a la antena, luego se puede volver a definir la Eficiencia de Reflexión como 1 - módulo del Coeficiente de reflexión2 , siendo el coeficiente de reflexión el cociente entre la diferencia de la impedancia de la antena y la impedancia de la línea de transmisión, y la suma de las mismas impedancias. Eficiencia de Reflexión = 1 - (Coeficiente de Reflexión)2 , donde Algunas veces se define la Eficiencia Total, siendo esta el producto entre la Eficiencia de Radiación y la Eficiencia de Reflexión. Eficiencia Total = Eficiencia de Radiación x Eficiencia de Reflexión Otra forma de calcular la eficiencia de una antena es utilizando la figura siguiente, en la que se muestra un circuito equivalente eléctrico simplificado para una antena. Parte de la potencia de entrada se disipa en las resistencias efectivas (resistencia de tierra, dieléctricos imperfectos, etc.) y la restante se irradia. El total de la potencia de la antena es la suma de las potencias disipada y radiada. En términos de resistencia y corriente, la eficiencia es: donde: n = eficiencia de la antena i = corriente de la antena Rr = resistencia de radiación Re = resistencia de la antena efectiva Patrón de Radiación En algunas circunstancias es necesario la representación gráfica de la fase del campo eléctrico. Esta representación recibe el nombre de Diagrama de Fase o Patrón de Radiación. Un patrón de radiación es un diagrama polar o gráfica que representa las intensidades de los campos o las densidades de potencia en varias posiciones angulares en relación con una antena. Si el patrón de radiación se traza en términos de la intensidad del campo eléctrico (E) o de la densidad de potencia (P), se llama patrón de radiación absoluto. Si se traza la intensidad del campo o la densidad de potencia en relación al valor en un punto de referencia, se llama patrón de radiación relativo. Algunas veces no nos interesa el diagrama de radiación en tres dimensiones, al no poder hacerse mediciones exactas sobre el. Lo que se suele hacer es un corte en el diagrama de radiación en tres dimensiones para pasarlo a dos dimensiones. Este tipo de diagrama es el más habitual ya que es más fácil de medir y de interpretar. Campos Cercanos y Lejanos El campo de radiación que se encuentra cerca de una antena no es igual que el campo de radiación que se encuentra a gran distancia. El termino campo cercano se refiere al patrón de campo que esta cerca de la antena, y el termino campo lejano se refiere al patrón de campo que está a gran distancia. Durante la mitad del ciclo, la potencia se irradia desde una antena, en donde parte de la potencia se guarda temporalmente en el campo cercano. Durante la segunda mitad del ciclo, la potencia que esta en el campo cercano regresa a la antena. Esta acción es similar a la forma en que un inductor guarda y suelta energía. Por tanto, el campo cercano se llama a veces campo de inducción. La potencia que alcanza el campo lejano continua irradiando lejos y nunca regresa a la antena por lo tanto el campo lejano se llama campo de radiación. La potencia de radiación, por lo general es la mas importante de las dos-, por consiguiente, los patrones de radiación de la antena, por lo regular se dan para el campo lejano. El campo cercano se define como el área dentro de una distancia D2/l de la antena, en donde l es la longitud de onda y D el diámetro de la antena en las mismas unidades. Ganancia Directiva y Ganancia de Potencia La ganancia directiva es la relación de la densidad de potencia radiada en una dirección en particular con la densidad de potencia radiada al mismo punto por una antena de referencia, suponiendo que ambas antenas irradian la misma cantidad de potencia. El patrón de radiación para la densidad de potencia relativa de una antena es realmente un patrón de ganancia directiva si la referencia de la densidad de potencia se toma de una antena de referencia estándar, que por lo general es una antena isotrópica. La máxima ganancia directiva se llama directividad. Matemáticamente, la ganancia directiva es: donde: D = ganancia directiva (sin unidades) P = densidad de potencia en algún punto de una antena determinada (W/m2) Pref = densidad de potencia en el mismo punto de una antena de referencia (W/m2) La ganancia de potencial es igual a la ganancia directiva excepto que se utiliza el total de potencia que alimenta a la antena (o sea, que se toma en cuenta la eficiencia de la antena). Se supone que la antena indicada y la antena de referencia tienen la misma potencia de entrada y que la antena de referencia no tiene perdidas (h = 100%). Matemáticamente, la ganancia de potencia (Ap) es: Ap = D h Si una antena no tiene perdidas, irradia 100% de la potencia de entrada y la ganancia de potencia es igual a la ganancia directa. La ganancia de potencia para una antena también se da en decibeles en relación con alguna antena de referencia. Por lo tanto, la ganancia de potencia es: Polarización de la Antena La polarización de una antena se refiere solo a la orientación del campo eléctrico radiado desde ésta. Una antena puede polarizarse en forma lineal (por lo general, polarizada horizontal o vertical), en forma elíptica o circular. Si una antena irradia una onda electromagnética polarizada verticalmente, la antena se define como polarizada verticalmente; si la antena irradia una onda electromagnética polarizada horizontalmente, se dice que la antena está polarizada horizontalmente; si el campo eléctrico radiado gira en un patrón elíptico, está polarizada elípticamente; y si el campo eléctrico gira en un patrón circular, está polarizada circularmente. Ancho del Haz de la Antena El ancho del haz de la antena es sólo la separación angular entre los dos puntos de media potencia (-3dB) en el lóbulo principal principal del patrón de radiación del plano de la antena, por lo general tomando en uno de los planos "principales". El ancho del haz para una antena cuyo patrón de radiación se muestra en la figura siguiente es el ángulo formado entre los puntos A, X y B ( ángulo q ). Los puntos A y B son los puntos de media potencia (la densidad de potencia en estos puntos es la mitad de lo que es, una distancia igual de la antena en la dirección de la máxima radiación). El ancho de haz de la antena se llama ancho de haz de -3dB o ancho de haz de media potencia. Ancho de Banda de la Antena El ancho de banda de la antena se define como el rango de frecuencias sobre las cuales la operación de la antena es "satisfactoria". Esto, por lo general, se toma entre los puntos de media potencia, pero a veces se refiere a las variaciones en la impedancia de entrada de la antena. Una antena es un dispositivo formado por un conjunto de conductores que, unido a un generador, permite la emisión de ondas de radio frecuencia, o que, conectado a una impedancia, sirve para captar las ondas emitidas por una fuente lejana para este fin existen diferentes tipos: Antena colectiva: Antena receptora que, mediante la conveniente amplificación y el uso de distribuidores, permite su utilización por diversos usuarios. Antena de cuadro: Antena de escasa sensibilidad, formada por una bobina de una o varias espiras arrolladas en un cuadro, cuyo funcionamiento bidireccional la hace útil en radiogoniometría. Antena de reflector o parabólica: Antena provista de un reflector metálico, de forma parabólica, esférica o de bocina, que limita las radiaciones a un cierto espacio, concentrando la potencia de las ondas; se utiliza especialmente para la transmisión y recepción vía satélite. Antena lineal: La que está constituida por un conductor rectilíneo, generalmente en posición vertical. Antena multibanda: La que permite la recepción de ondas cortas en una amplitud de banda que abarca muy diversas frecuencias. Dipolo de Media Onda El dipolo de media onda lineal o dipolo simple es una de las antenas más ampliamente utilizadas en frecuencias arriba de 2MHz. En frecuencias abajo de 2 MHz, la longitud física de una antena de media longitud de onda es prohibitiva. Al dipolo de media onda se le refiere por lo general como antena de Hertz. Una antena de Hertz es una antena resonante. O Sea, es un múltiplo de un cuarto de longitud de onda de largo y de circuito abierto en el extremo más lejano. Las ondas estacionarias de voltaje y de corriente existen a lo largo de una antena resonante. La figura anterior podemos observar las distribuciones de corriente y voltaje ideales a lo largo de un dipolo de media onda. Cada polo de la antena se ve como una sección abierta de un cuarto de longitud de onda de una linea de transmisión. Por lo tanto en los extremos hay un máximo voltaje y un mínimo de corriente y un mínimo de voltaje y un máximo de corriente en el centro. La impedancia varia de un valor máximo en los extremos de aproximadamente 2500 W a un valor mínimo en el punto de alimentación de aproximadamente 73 W (de los cuales entre 68 y 70 W es la impedancia de radiación). El patrón de radiación de espacio libre para un dipolo de media onda depende de la localización horizontal o vertical de la antena con relación a la superficie de la tierra. La figura siguiente muestra el patrón de radiación vertical para un dipolo de media onda montado verticalmente. Observese que los dos lóbulos principales que irradian en direcciones opuestas están en ángulo derecho a la antena, los lóbulos no son círculos, se obtienen solo en el caso ideal donde la corriente es constante a todo lo largo de la antena, y esto es inalcanzable en una antena real. Antena Yagi: Antena constituida por varios elementos paralelos y coplanarios, directores, activos y reflectores, utilizada ampliamente en la recepción de señales televisivas. Los elementos directores dirigen el campo eléctrico, los activos radian el campo y los reflectores lo reflejan. (figura siguiente) Los elementos no activados se denominan parásitos, la antena yagi puede tener varios elementos activos y varios parásitos. Su ganancia esta dada por: G = 10 log n donde n es el número de elementos por considerar. Para la antena yagi de tres elementos la distancia entre el reflector y el activo es de 0.15l , y entre el activo y el director es de 0.11l . Estas distancias de separación entre los elementos son las que proporcionan la óptima ganancia, ya que de otra manera los campos de los elementos interferirían destructivamente entre sí, bajando la ganancia. Como se puede observar, este diseño de antena yagi resulta ser de ancho de banda angosto, ya que el elemento dipolar está cortado a una sola frecuencia que generalmente se selecciona en la mitad del ancho de banda de los canales bajos de TV; es decir, del canal 2 al canal 6 (de 50MHz a 86 MHz). Esto resulta ser una desventaja ya que no es posible cubrir varios canales de TV con una misma ganancia seleccionada. Por tal razón se utiliza la denominada antena yagi de banda ancha, la cual puede cubrir varios canales a la vez aunque sacrificando la ganancia. En la figura siguiente se muestran los parámetros de diseño x y y, creando la relación x + y = l /4, la ganancia se acentúa alrededor de un solo canal, como se muestra en la figura. Para considerar una antena yagi de banda ancha es necesario, entonces, hacer ajustes en las distancia entre los elementos para obtener, junto con el ancho de banda deseado, la ganancia óptima. Se recuerda que para un arreglo de antenas en las cuales todos los elementos van alimentados se obtiene mejor ganancia para el denominado "en linea". Como la antena yagi utiliza elementos alimentados y parasitos, es común aumentar el numero de elementos alimentados a 2 o 3; estos dipolos se cortan a la frecuencia media del ancho de banda; generalmente para los canales bajos de televisión da muy buen resultado. En la figura siguiente se proporciona las dimensiones para óptima ganancia de una antena yagi de tres elementos Antenas Vhf Y Uhf Para clasificar las ondas de radio se toman como medida los múltiplos de diez en la longitud de onda. Por lo tanto la ondas de VHF tienen una longitud de onda entre 1 Metro y 10 Metros mientras que las de UHF tienen una longitud de entre 10 Centímetros y un Metro. Como la relación es que la frecuencia es igual a la velocidad de la luz (misma velocidad que la de propagación de las ondas electromagnéticas, aproximadamente 300.000 Km./h) dividida por la longitud de onda, entonces tenemos que la banda de VHF va desde los 30 Mhz a los 300 Mhz y la de UHF va de los 300 Mhz a los 3 Ghz. Las actuales aplicaciones en comunicaciones de punto a punto o móviles que superan los 30 Mhz son muy populares y han hecho que aparezcan un gran numero de antenas para estas aplicaciones. La figura ilustran algunos tipos de antenas buenas para polarizaciones eléctricas verticales y fáciles de montar en un mástil. Excepto por un aislante que esta señalado como "insulator" en la figura todas las demás líneas son de materiales conductores ya que para una representación simple se han obviado los aislantes. 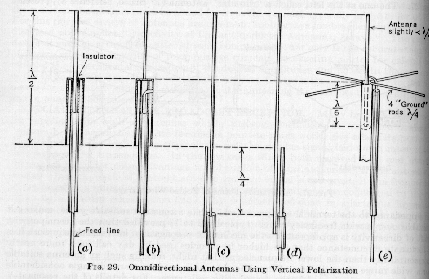 La parte mas baja de (a) es el coaxial que alimenta media longitud de onda de la parte superior de la antena en el medio en una conexión en serie (Toda la corriente de la línea de alimentación fluye a través de la antena). La porción de diámetro ancho no toca el conductor exterior de la línea de alimentación excepto en la punta, esto es una condición que tiende a minimizar que las ondas se queden el mástil que sostiene a la antena. En la antena (b) vemos que hay una conexión entre la parte interna y las partes adyacentes, la alimentación esta perfeccionada por traer el conductor interior de la línea de alimentación a través de un agujero al exterior en un punto dentro del aislamiento que esta protegido del clima. En la antena (c) y (d) son dos antenas en forma de "J" en las que la sección radiante es la media onda superior de una de las líneas de alimentación sobre el punto en que la otra termina. En la figura (e) se ve una cruz horizontal de cuatro caños tierra sobre un largo cilindro, en el final hueco del cual esta montado el conductor interno que se extiende sobre el un poco menos que un cuarto de onda, se pone el punto de conexión coaxial de tal manera que coincidan las impedancias. La sección que continua este punto de conexión provee un fuerte soporte mecánico a la parte radiante por sobre ella. Cuando se usa polarización horizontal en transmisiones de UHF hay muchos tipos de antenas a ser considerados. En esta polarización es mas fácil incrementar la ganancia que en la vertical por el método de "Stacking" (apilar). Muchos tipos están indicados en la siguiente figura. 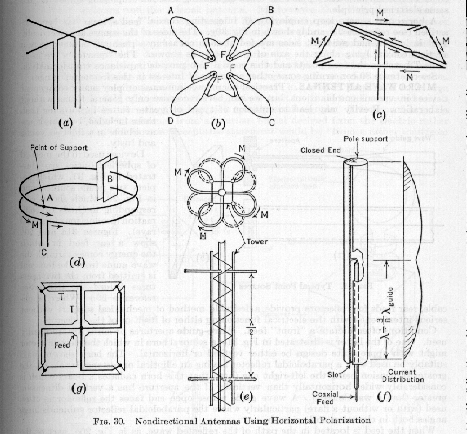 La "Tunrstile" que es la mostrada en el punto (a). Esencialmente tiene dos partes radiantes con una longitud de media onda desfasadas 90º y puestas en fases de cuadratura. Esta alimentada por un sistema de alimentación de líneas de transmisión. Cuando corrientes iguales son usadas en dos radiadores, el diagrama direcciones en el plano horizontal es un circulo deformado que va tendiendo a un cuadrado. La separación vertical entre elementos apilados es de media onda. La antena Turnstile esta adaptada para el uso de una banda de transmisión por el empleo de conductores largos y un cuidado extremo de todos los detalles. Una sección cruzada de dicha antena esta mostrada en la figura (B) donde se ve una antena usada en el Empire State, donde los conductores con diámetros de un cigarrillo y las partes adyacentes centradas son superficies de revoluciones sobre las líneas AC y BD. Líneas separadas de transmisión son proveídas en F para cada uno de los cuatro radiadores. La figura (C) es un "Aldorf Loop" que es en forma de cuadrado, donde el largo de cuyo vértice es una cuestión de diseño, pero por propósitos descriptivos puede ser tomado por aproximadamente un tercio de longitud de onda. La corriente es entregada como se muestra en la figura, las corrientes en los cuatro radiadores son iguales en magnitud y parecidas en fase como se muestra en las flechas del diagrama. En apilamiento en un espacio vertical se usa una distancia de media onda. La figura (d) muestra una antena circular que también se llama antena de loop. Los dos conductores circulares radiantes están eléctricamente rotos en B por un condensador plano paralelo sin perdida de continuidad mecánica y de fuerza, toda la construcción es capaz de ser soportada desde el punto A. El circulo mas bajo esta roto en C, de donde el sistema es alimentado en la forma de "Folded Dipole" (Dipolo Doblado) el "largo eléctrico" de la circunferencia (Tomando en cuenta la carga capacitiva de B) es de media onda. Físicamente la circunferencia es menos que esto. Esta antena esta enganchada a un mástil en el punto A y por lo tanto metálicamente a tierra. El mástil esta dentro de la circunferencia. La forma direcciones horizontal es elíptica, la máxima diferencia en campo de fuerza es un poco menos que 2 db. Cuando estas unidades están apiladas en vertical el espacio entre ellas es de una longitud de onda. La antena "Coverleaf"esta mostrada en la figura (e). Esta consiste en una torre de estructura metálica delgada. En el centro hay un conductor que junto con la torre misma forman un sistema de transmisión coaxial. Las "Hojas" radiantes están agarradas como se muestra en la figura, formando una circunferencia horizontal compuesta. El largo de cada uno de estos conductores el de aproximadamente 0.4 de longitud de onda. En apilamientos se usan intervalos de media longitud de onda. El diagrama horizontal prácticamente circular. La antena Cohete que se muestra en la figura (f), es un cilindro vertical cerrado metálicamente en sus dos extremos, pero tiene una grieta abierta en un elemento del cilindro como muestra la figura (slot), Esta alimentado como se muestra en el lugar donde se ve un corte en el cilindro estableciendo un voltaje a través de la grieta. La antena tiene un efecto externo como una distribución vertical de circunferencias horizontales. Las unidades apiladas son puestas muy juntas. El diámetro es mas o menos que media longitud de onda. La figura (g) es una antena de circunferencia horizontal que tiene un particular sistema de alimentación coaxial. Las antenas de VHF y UHF también se puede clasificar en cuatro categorías dependiendo de otros parámetros como se ve en la siguiente tabla.  Cada una de estos tipos de antenas tiene asociadas formas de antenas especificas del mismo. Algunas de estas formas de antena fueron mencionadas o explicadas con anterioridad.  Ajuste de antenas de VHF y UHF Es un error pensar que, disponiendo excelente medidor de R.O.E., y comprobando que estamos con antenas ajustadas a 1:1, la ganancia será la que creemos por la cantidad de elementos de la antena. Una yagui cruzada de 7 + 7 elementos, con una ganancia teórica en 11 db cada una, según tablas de Radio-Amateur Handbook, resultaron al ser medidas de 6 db una y 3 db la otra y la R.O.E. era de 1:1,10 en ambas. El método simple y realmente efectivo es medir la intensidad de campo. Ajustar la antena con una señal lejana es algo complicado, ya que se debe contar con un colega que mantenga una transmisión constante por tiempo considerable, además de violar la reglamentación. Para medir la intensidad de campo conviene fijar el transmisor con potencia baja, y es necesario cerciorarse que el equipo transmita con la misma potencia en las distintas frecuencias de la banda. Una antena terminada y ajustada para mínima R.O.E., se ajustara para máxima ganancia con la ayuda de un medidor de intensidad de campo Vanessa Gaviria CAF |
Etiquetas:
Vanessa Gaviria
Representación de Formas de onda
Forma de onda significa la forma y la forma de a señal por ejemplo a onda moviéndose en un medio sólido, líquido o gaseoso.  En muchos casos el medio en el cual se está propagando la onda no permite una imagen visual directa de la forma. En estos casos, el término "forma de onda" refiere a la forma de un gráfico de la cantidad que varía contra tiempo o distancia. Un instrumento llamado osciloscopio se puede utilizar pictorially para representar la onda como imagen la repetición en a CRT o LCD pantalla. Por la extensión del antedicho, el término "forma de onda" ahora también se utiliza a veces para describir la forma del gráfico de cualquier cantidad que varía contra tiempo
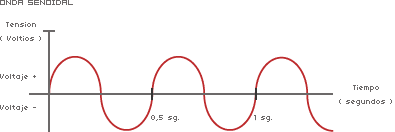
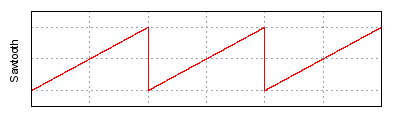

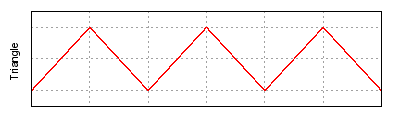 Otras formas de onda se llaman las formas de onda compuestas y se pueden a menudo describir a menudo como combinación de un número de ondas sinusoidales o de otra funciones de la base agregado junto. Serie de Fourier describe la descomposición de las formas de onda periódicas, tales que cualquier forma de onda periódica se puede formar por la suma de componentes componentes y armónicos fundamentales. las formas de onda no-periódicas de la Finito-energía se pueden analizar en sinusoids por Fourier transforma. Vanessa Gaviria CAF |
Etiquetas:
Vanessa Gaviria
Introduccion a Señales
Este texto está diseñado para el primer o segundo año de ingeniería con especialidad en comunicaciones (telecomunicaciones), computadores, software o en el área de la electricidad/electrónica. Se cubre la manipulación básica de señales, propiedades de las señales, convolución, trasformadas de Fourier y otro material apropiado para nivel de principiantes en el Análisis de Señales. La meta de todo esto, es aprender acerca del diseño de sistemas eléctricos. Todos los métodos en este libro son concernientes a encontrar la salida de un sistema para una entrada dada. La convolución puede ser pensada como un método de fuerza bruta para lograr esto, mientras que los otros métodos convierten la señal desde el dominio del tiempo, al dominio de la frecuencia, donde calcular la salida es mucho más fácil. Una vez que todo este material básico ya esté cubierto, entonces se cubrirá el material restante(por cierto más interesante), por ejemplo filtros, el dominio de la frecuencia, la relación entre ancho de banda y el dominio del tiempo, la compresión de audio, porqué los cd muestrean a 44.1 KHz, etc. Mi objetivo al igual que Mr. Wilkinson es crear un libro básico de señales y sistemas, a lo que agrego algunos tópicos de control automáticos que me parezcan interesantes. Este texto es un primer aporte y pido, por anticipado disculpas por todos los errores que en él se encuentren, errores que espero corregir con el tiempo. Igualmente pido disculpas a Mr. Wilkinson por haber usado el material que él ha escrito como punto de partida. Por ahora el texto solamente corresponde a una traducción del original en inglés, en una segunda etapa de desarrollo me permitiré cambiar el orden y los tópicos que en él se utilicen para mejorarlo lo más que pueda. Herramientas Básicas En esta sección encontrará algunos detalles acerca de los términos utilizados en este libro. También encontrará algunos enlaces de interés a libros externos o sitios web que cubren algunos tópicos más profundamente de lo que se tratan aquí. TerminologíaFunciones de SingularidadLas funciones de singularidad son un grupo de funciones que están relacionadas con la función impulso. Aparte de la función impulso están la función escalón y la función rampa Función ImpulsoLa función impulso es más un concepto matemático que una función, que se define de la siguiente manera:
La función impulso posee algunas propiedades que pueden resultar útiles. También es importante para posteriores desarrollos la propiedad de desplazamiento o corrimiento. Fisicamente existen efectos en la naturaleza a los que se puede asociar esta funcion como por ejemplo la fuerza aplicada en un lapso muy corto, como cuando un martillo golpea un clavo, o la presencia de un voltaje por un instante muy corto que en terminos de esta funcion como:
Función Escalón UnitarioLa función escalón unitario se define como la integral de la función impulso desde el infinito negativo hasta el tiempo. la integral de la función impulso es 0 si el tiempo t es menor que 0, y 1 si el tiempo t es mayor que se define exactamente el escalón unitario. el tipo de escalón unitario corresponde a una salida. El valor de la función en t=0, es indefinido. Otros textos lo pueden definir como 1 o 0. Así pues ésta nos representa la corriente continua disipada en nuestro dispositivo. En el caso de la funcion escalón, fisicamente representa un cambio instantáneo que se produce a t=0, es una suposición el hecho de representar una funcion con tiempos negativos (lo cual no existe), en cambio sirve para representar el caso de un interruptor que permanece abierto hasta que en un instante se cierra, estableciendo el máximo voltaje a una carga. Función RampaLa función rampa es la integral de la función escalón. Si consideramos que estamos sumando toda el área bajo la función escalón a hasta un tiempo t. Si t < 0 (cero), el valor de la integral será 0 (cero). Si es mayor que 0 (cero) , entonces el valor será igual a la integral de 1 desde el tiempo 0 hasta el tiempo t, la cual también tiene el valor t, es decir: Relación existente entre estas señalesRelación Impulso / EscalónTal como se puede fácilmente demostrar, la función escalón y la función impulso están relacionados de la siguiente manera:  y  Relación Escalón / RampaVisto desde el punto de vista matemático una es la derivada de la otra puesto que; la función rampa se deriva de la funcion escalón, y ésta a su vez de la impulso. Análogamente igualmente se demuestra que  y  SeñalesLas señales son parte integrante de un todo. Las señales no tienen significado sin sistemas que las interpreten, y los sistemas son inútiles sin señales que procesar. Este capítulo profundiza en las señales: ¿qué son?, ¿cuáles son? y ¿cuáles son sus propiedades? Estas propiedades se usan para describir características de las señales. También se cubren temas de transformaciones de señales, estas transformaciones son sólo matemáticas (conceptualmente se transforman la señal, no se diseñará un sistema para hacerlo). Por ejemplo la inversión en el dominio del tiempo es una transformación. Una señal es cualquier fenómeno que puede ser representado de manera cuantitativa mediante una función continua (cuyo dominio es los números reales) o discreta (cuyo dominio es los números enteros). Como ejemplos de señales se tienen: La variación de la presión de aire a la salida de un parlante. La variación de la intensidad electromagnética que llega a una antena receptora. La variación de la temperatura máxima tomada diariamente. Los colores de una imagen digitalizada (pixeles). Señales ContinuasUna señal continua es una señal "suave" que está definida para todos los puntos de un intervalo determinado del conjunto de los números reales. Por ejemplo, la función seno es un ejemplo continuo, como la función exponencial o la función constante. Una parte de la función seno en el rango de tiempos de 0 a 6 segundos también es contínua. Si deseamos ejemplos de la naturaleza tenemos la corriente, el voltaje, el sonido, la luz, etc. Señales DiscretasUna señal discreta es una señal discontinua que está definida para todos los puntos de un intervalo determinado del conjunto de los números enteros. Su importancia en la tecnología es que, los computadores y microchips que son utilizados en este nuevo mundo "Digital" en el que vivimos, sólo manejan señales discretas. Una señal discreta en la naturaleza podría ser el pulso cardíaco, el rebotar de una pelota al caer libremente, etc. Si para todos los valores de una variable existe un valor, estamos hablando de una señal continua. Parte Par e Impar de una señal
Transformaciones de Señales Continuas Simples
Amplificación, Atenuación, Limitación, (falta definir cada una de éstas). Amplificación:es aumentar el "tamaño" de una señal mediante diferentes equipos para poder hacer mediciones y/o operaciones con las señales.
Compresión, Expansión y Escalamiento Temporales (falta definir cada una de éstas).
Una inversión de signo voltea la señal a lo largo del eje de amplitud. Asi, "los últimos serán los primeros y los primeros serán los últimos." Las tres funciones básicas se modifican como sigue:
Sistemas Lineales Invariantes en el Tiempo (LIT)Se dice que un sistema lineal es invariante en el tiempo si un desplazamiento en el tiempo de la entrada resulta en un desplazamiento idéntico de la salida sin que cambie la forma de onda o perfil de la señal. Esto se puede enunciar en la forma siguiente: Un sistema lineal es invariante en el tiempo si para cualquier desplazamiento  se verifica que se verifica que , ,y como consecuencia, para cualquier señal 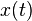 y desplazamiento y desplazamiento  , , . .Por consiguiente, en un Sistema Lineal Invariante en el Tiempo (LIT), la respuesta impulsional dependerá únicamente de la diferencia  , es decir, , es decir,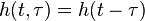 La respuesta de un LIT es entonces el producto de convolución de la excitación con la respuesta impulsional del sistema.DISCRETOS ConvoluciónConvolución de Señales en Sistemas Continuos LTISe define a la integral de convolución  Y la respuesta de un sistema lineal estacionario a una entrada arbitraria se obtiene como la convolucion entre la entrada y la respuesta al impulso. Si el sistema es causal Y la respuesta de un sistema lineal estacionario a una entrada arbitraria se obtiene como la convolucion entre la entrada y la respuesta al impulso. Si el sistema es causal  donde la primera intregral depende de valores futuros y la segunda de valores pasados y presentes por lo que si el sistema es casual la convolución queda definida como donde la primera intregral depende de valores futuros y la segunda de valores pasados y presentes por lo que si el sistema es casual la convolución queda definida como  EjemplosConvolución de una rampa con un pulso y(t) = r(t) * u(t)  luego como la rampa r(t)=t*u(t) reemplazamos en la integral  y como U(τ) vale 0 en los valores negativos ya tenemos uno de los límites de integración y si aparte consideramos que a u(t − τ) lo despejamos y lo corremos t veces el otro límite de integracion queda definido por el valor t. quedando la fórmula de esta manera  la cual es muy fácil de integrar obteniendo así la cual es muy fácil de integrar obteniendo así Series y Transformadas de FourierSeries de FourierMuchas aplicaciones de ingeniería involucran el procesamiento de señales aleatorias. Algunos ejemplos de estas aplicaciones son: predicción, donde obtenemos futuros valores de una señal usando valores pasados de la misma; filtrado, donde buscamos recuperar los valores de una señal que ha sido alterada por ruido; modulación, donde convertimos señales de información de bajas frecuencias en señales de transmisión de alta frecuencia que se transmiten más fácilmente en el medio de transmisión. En todos estos casos, el procesamiento de las señales involucra convertir una señal en otra. Es decir que se efectúa una transformación o mapeo de una función del tiempo (la señal de entrada) en otra función del tiempo (la señal de salida). Esta transformación está representada por un sistema dinámico. En estas notas estamos interesados en describir las propiedades estadísticas de la señal de salida cuando el sistema es lineal e invariante en el tiempo, y la señal de entrada es estacionaria en sentido amplio. Somero repaso de Señales y Sistemas Un sistema dinámico es una transformación entre el espacio de señales de entrada y el espacio de señales de salida. pendiente por que no aparece la explicacion de espacio dinamico Soluciones de Fourier en el Dominio de la FrecuenciaEjemplos11 las derivadas de las señales sinousidales dependen del numero de frecuencia de forma analogica segun la señal si es discreta y continua, que basicamente una señal discreta tambien cuenta con una señal continua. Transformada de LaplaceLa transformada de Laplace es una transformación matemática. Nos ayuda a resolver sistemas complejos mediante la transformación de dichos sistemas en ecuaciones algebraicas sencillas. Por ejemplo, en vez de usar ecuaciones diferenciales, mediante la transformada de Laplace, convertimos dichas ecuaciones en polinomios, que son de menor dificultad resolutiva. Tabla de Transformadas de FourierVanessa GaviriaCAFhttp://es.wikibooks.org/wiki/Introducci%C3%B3n_a_Se%C3%B1ales,_Sistemas_y_Control |
Etiquetas:
Vanessa Gaviria
Suscribirse a:
Comentarios (Atom)



















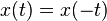 . Es decir, esta función presenta una simetría en torno al eje
. Es decir, esta función presenta una simetría en torno al eje 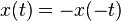 . Es decir, esta función presenta una simetría respecto al origen del sistema de coordenadas. (Espejo a través de la recta
. Es decir, esta función presenta una simetría respecto al origen del sistema de coordenadas. (Espejo a través de la recta  )
)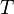 cumpliéndose que
cumpliéndose que  . Por ejemplo, una onda cuadrada o sinusoidal son ondas periódicas, en tanto que la función
. Por ejemplo, una onda cuadrada o sinusoidal son ondas periódicas, en tanto que la función  no es periódica.
no es periódica. queda igual
queda igual se transforma en
se transforma en 
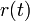 se transforma en
se transforma en 