Este texto está diseñado para el primer o segundo año de ingeniería con especialidad en comunicaciones (telecomunicaciones), computadores, software o en el área de la electricidad/electrónica. Se cubre la manipulación básica de señales, propiedades de las señales, convolución, trasformadas de Fourier y otro material apropiado para nivel de principiantes en el Análisis de Señales. La meta de todo esto, es aprender acerca del diseño de sistemas eléctricos. Todos los métodos en este libro son concernientes a encontrar la salida de un sistema para una entrada dada. La convolución puede ser pensada como un método de fuerza bruta para lograr esto, mientras que los otros métodos convierten la señal desde el dominio del tiempo, al dominio de la frecuencia, donde calcular la salida es mucho más fácil. Una vez que todo este material básico ya esté cubierto, entonces se cubrirá el material restante(por cierto más interesante), por ejemplo filtros, el dominio de la frecuencia, la relación entre ancho de banda y el dominio del tiempo, la compresión de audio, porqué los cd muestrean a 44.1 KHz, etc. Mi objetivo al igual que Mr. Wilkinson es crear un libro básico de señales y sistemas, a lo que agrego algunos tópicos de control automáticos que me parezcan interesantes. Este texto es un primer aporte y pido, por anticipado disculpas por todos los errores que en él se encuentren, errores que espero corregir con el tiempo. Igualmente pido disculpas a Mr. Wilkinson por haber usado el material que él ha escrito como punto de partida. Por ahora el texto solamente corresponde a una traducción del original en inglés, en una segunda etapa de desarrollo me permitiré cambiar el orden y los tópicos que en él se utilicen para mejorarlo lo más que pueda. Herramientas Básicas En esta sección encontrará algunos detalles acerca de los términos utilizados en este libro. También encontrará algunos enlaces de interés a libros externos o sitios web que cubren algunos tópicos más profundamente de lo que se tratan aquí. TerminologíaFunciones de SingularidadLas funciones de singularidad son un grupo de funciones que están relacionadas con la función impulso. Aparte de la función impulso están la función escalón y la función rampa Función ImpulsoLa función impulso es más un concepto matemático que una función, que se define de la siguiente manera:
La función impulso posee algunas propiedades que pueden resultar útiles. También es importante para posteriores desarrollos la propiedad de desplazamiento o corrimiento. Fisicamente existen efectos en la naturaleza a los que se puede asociar esta funcion como por ejemplo la fuerza aplicada en un lapso muy corto, como cuando un martillo golpea un clavo, o la presencia de un voltaje por un instante muy corto que en terminos de esta funcion como:
Función Escalón UnitarioLa función escalón unitario se define como la integral de la función impulso desde el infinito negativo hasta el tiempo. la integral de la función impulso es 0 si el tiempo t es menor que 0, y 1 si el tiempo t es mayor que se define exactamente el escalón unitario. el tipo de escalón unitario corresponde a una salida. El valor de la función en t=0, es indefinido. Otros textos lo pueden definir como 1 o 0. Así pues ésta nos representa la corriente continua disipada en nuestro dispositivo. En el caso de la funcion escalón, fisicamente representa un cambio instantáneo que se produce a t=0, es una suposición el hecho de representar una funcion con tiempos negativos (lo cual no existe), en cambio sirve para representar el caso de un interruptor que permanece abierto hasta que en un instante se cierra, estableciendo el máximo voltaje a una carga. Función RampaLa función rampa es la integral de la función escalón. Si consideramos que estamos sumando toda el área bajo la función escalón a hasta un tiempo t. Si t < 0 (cero), el valor de la integral será 0 (cero). Si es mayor que 0 (cero) , entonces el valor será igual a la integral de 1 desde el tiempo 0 hasta el tiempo t, la cual también tiene el valor t, es decir: Relación existente entre estas señalesRelación Impulso / EscalónTal como se puede fácilmente demostrar, la función escalón y la función impulso están relacionados de la siguiente manera:  y  Relación Escalón / RampaVisto desde el punto de vista matemático una es la derivada de la otra puesto que; la función rampa se deriva de la funcion escalón, y ésta a su vez de la impulso. Análogamente igualmente se demuestra que  y  SeñalesLas señales son parte integrante de un todo. Las señales no tienen significado sin sistemas que las interpreten, y los sistemas son inútiles sin señales que procesar. Este capítulo profundiza en las señales: ¿qué son?, ¿cuáles son? y ¿cuáles son sus propiedades? Estas propiedades se usan para describir características de las señales. También se cubren temas de transformaciones de señales, estas transformaciones son sólo matemáticas (conceptualmente se transforman la señal, no se diseñará un sistema para hacerlo). Por ejemplo la inversión en el dominio del tiempo es una transformación. Una señal es cualquier fenómeno que puede ser representado de manera cuantitativa mediante una función continua (cuyo dominio es los números reales) o discreta (cuyo dominio es los números enteros). Como ejemplos de señales se tienen: La variación de la presión de aire a la salida de un parlante. La variación de la intensidad electromagnética que llega a una antena receptora. La variación de la temperatura máxima tomada diariamente. Los colores de una imagen digitalizada (pixeles). Señales ContinuasUna señal continua es una señal "suave" que está definida para todos los puntos de un intervalo determinado del conjunto de los números reales. Por ejemplo, la función seno es un ejemplo continuo, como la función exponencial o la función constante. Una parte de la función seno en el rango de tiempos de 0 a 6 segundos también es contínua. Si deseamos ejemplos de la naturaleza tenemos la corriente, el voltaje, el sonido, la luz, etc. Señales DiscretasUna señal discreta es una señal discontinua que está definida para todos los puntos de un intervalo determinado del conjunto de los números enteros. Su importancia en la tecnología es que, los computadores y microchips que son utilizados en este nuevo mundo "Digital" en el que vivimos, sólo manejan señales discretas. Una señal discreta en la naturaleza podría ser el pulso cardíaco, el rebotar de una pelota al caer libremente, etc. Si para todos los valores de una variable existe un valor, estamos hablando de una señal continua. Parte Par e Impar de una señal
Transformaciones de Señales Continuas Simples
Amplificación, Atenuación, Limitación, (falta definir cada una de éstas). Amplificación:es aumentar el "tamaño" de una señal mediante diferentes equipos para poder hacer mediciones y/o operaciones con las señales.
Compresión, Expansión y Escalamiento Temporales (falta definir cada una de éstas).
Una inversión de signo voltea la señal a lo largo del eje de amplitud. Asi, "los últimos serán los primeros y los primeros serán los últimos." Las tres funciones básicas se modifican como sigue:
Sistemas Lineales Invariantes en el Tiempo (LIT)Se dice que un sistema lineal es invariante en el tiempo si un desplazamiento en el tiempo de la entrada resulta en un desplazamiento idéntico de la salida sin que cambie la forma de onda o perfil de la señal. Esto se puede enunciar en la forma siguiente: Un sistema lineal es invariante en el tiempo si para cualquier desplazamiento  se verifica que se verifica que , ,y como consecuencia, para cualquier señal 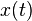 y desplazamiento y desplazamiento  , , . .Por consiguiente, en un Sistema Lineal Invariante en el Tiempo (LIT), la respuesta impulsional dependerá únicamente de la diferencia  , es decir, , es decir,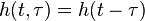 La respuesta de un LIT es entonces el producto de convolución de la excitación con la respuesta impulsional del sistema.DISCRETOS ConvoluciónConvolución de Señales en Sistemas Continuos LTISe define a la integral de convolución  Y la respuesta de un sistema lineal estacionario a una entrada arbitraria se obtiene como la convolucion entre la entrada y la respuesta al impulso. Si el sistema es causal Y la respuesta de un sistema lineal estacionario a una entrada arbitraria se obtiene como la convolucion entre la entrada y la respuesta al impulso. Si el sistema es causal  donde la primera intregral depende de valores futuros y la segunda de valores pasados y presentes por lo que si el sistema es casual la convolución queda definida como donde la primera intregral depende de valores futuros y la segunda de valores pasados y presentes por lo que si el sistema es casual la convolución queda definida como  EjemplosConvolución de una rampa con un pulso y(t) = r(t) * u(t)  luego como la rampa r(t)=t*u(t) reemplazamos en la integral  y como U(τ) vale 0 en los valores negativos ya tenemos uno de los límites de integración y si aparte consideramos que a u(t − τ) lo despejamos y lo corremos t veces el otro límite de integracion queda definido por el valor t. quedando la fórmula de esta manera  la cual es muy fácil de integrar obteniendo así la cual es muy fácil de integrar obteniendo así Series y Transformadas de FourierSeries de FourierMuchas aplicaciones de ingeniería involucran el procesamiento de señales aleatorias. Algunos ejemplos de estas aplicaciones son: predicción, donde obtenemos futuros valores de una señal usando valores pasados de la misma; filtrado, donde buscamos recuperar los valores de una señal que ha sido alterada por ruido; modulación, donde convertimos señales de información de bajas frecuencias en señales de transmisión de alta frecuencia que se transmiten más fácilmente en el medio de transmisión. En todos estos casos, el procesamiento de las señales involucra convertir una señal en otra. Es decir que se efectúa una transformación o mapeo de una función del tiempo (la señal de entrada) en otra función del tiempo (la señal de salida). Esta transformación está representada por un sistema dinámico. En estas notas estamos interesados en describir las propiedades estadísticas de la señal de salida cuando el sistema es lineal e invariante en el tiempo, y la señal de entrada es estacionaria en sentido amplio. Somero repaso de Señales y Sistemas Un sistema dinámico es una transformación entre el espacio de señales de entrada y el espacio de señales de salida. pendiente por que no aparece la explicacion de espacio dinamico Soluciones de Fourier en el Dominio de la FrecuenciaEjemplos11 las derivadas de las señales sinousidales dependen del numero de frecuencia de forma analogica segun la señal si es discreta y continua, que basicamente una señal discreta tambien cuenta con una señal continua. Transformada de LaplaceLa transformada de Laplace es una transformación matemática. Nos ayuda a resolver sistemas complejos mediante la transformación de dichos sistemas en ecuaciones algebraicas sencillas. Por ejemplo, en vez de usar ecuaciones diferenciales, mediante la transformada de Laplace, convertimos dichas ecuaciones en polinomios, que son de menor dificultad resolutiva. Tabla de Transformadas de FourierVanessa GaviriaCAFhttp://es.wikibooks.org/wiki/Introducci%C3%B3n_a_Se%C3%B1ales,_Sistemas_y_Control |
Electromagnetic Compatibility. EMC Requirements for Electronic Systems. Signal Spectra—the Relationship between the Time Domain and the Frequency Domain. Representation of Nonperiodic Waveforms. Transmission Lines and Signal Integrity. Nonideal Behavior of Components. Conducted Emissions and Susceptibility. Measurement of Conducted Emissions. Antennas. Elemental Dipole Antennas. Radiated Emissions and Susceptibility. Simple Emission Models for Wires and PCB Lands. Crosstalk.
lunes, 15 de febrero de 2010
Introduccion a Señales
Etiquetas:
Vanessa Gaviria
Suscribirse a:
Enviar comentarios (Atom)










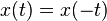 . Es decir, esta función presenta una simetría en torno al eje
. Es decir, esta función presenta una simetría en torno al eje 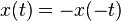 . Es decir, esta función presenta una simetría respecto al origen del sistema de coordenadas. (Espejo a través de la recta
. Es decir, esta función presenta una simetría respecto al origen del sistema de coordenadas. (Espejo a través de la recta  )
)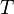 cumpliéndose que
cumpliéndose que  . Por ejemplo, una onda cuadrada o sinusoidal son ondas periódicas, en tanto que la función
. Por ejemplo, una onda cuadrada o sinusoidal son ondas periódicas, en tanto que la función  no es periódica.
no es periódica. queda igual
queda igual se transforma en
se transforma en 
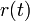 se transforma en
se transforma en 
No hay comentarios:
Publicar un comentario